Two solid spheres A and B of equal volumes but of different densities dA and dB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as show in the figure with a tension in the string. The arrangement is possible only if :

Engineering

Physics

Equilibrium

Buoyancy

Free Body Diagram

Question

Two solid spheres A and B of equal volumes but of different densities d_A and d_B are connected by a string. They are fully immersed in a fluid of density d_F. They get arranged into an equilibrium state as show in the figure with a tension in the string. The arrangement is possible only if :

d_A + d_B = 2d_F

d_A < d_F

d_B > d_F

d_A > d_F

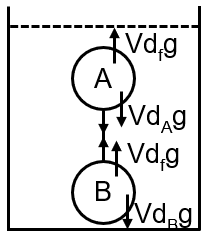
system will be in equilibrium with tension in string only if d_f > d_A and d_B > df. If both A & B are considered as a system then

2Vdfg = V (d_A + d_B)g $\Rightarrow$ d_A + d_B = 2d_f

This problem involves two spheres of equal volume but different densities connected by a string and fully immersed in a fluid. For the system to be in equilibrium with tension in the string, we must analyze the forces acting on each sphere.

Step 1: Identify Forces
For any object submerged in a fluid, two primary forces act:

Weight acting downward: $W = m g = d V g$ , where $d$ is density, $V$ is volume, and $g$ is gravity.
Buoyant force acting upward: $F_{B} = d_{F} V g$ , where $d_{F}$ is fluid density.

Since the volumes are equal, let

V

be the volume of each sphere.

Step 2: Analyze Equilibrium for Each Sphere
From the figure, sphere A is above sphere B. For equilibrium, the net force on each sphere must be zero.

For sphere A (top sphere):

Forces acting: Weight downward ( $W_{A} = d_{A} V g$ ), Buoyant force upward ( $F_{B A} = d_{F} V g$ ), Tension in string downward (since it is connected below).
Equilibrium equation: $F_{B A} = W_{A} + T$
Substituting: $d_{F} V g = d_{A} V g + T$
This implies $d_{F} > d_{A}$ for tension $T > 0$ .

For sphere B (bottom sphere):

Forces acting: Weight downward ( $W_{B} = d_{B} V g$ ), Buoyant force upward ( $F_{B B} = d_{F} V g$ ), Tension upward (since it is connected above).
Equilibrium equation: $F_{B B} + T = W_{B}$
Substituting: $d_{F} V g + T = d_{B} V g$
This implies $d_{B} > d_{F}$ for tension $T > 0$ .

Step 3: Combine the Equations
From sphere A: $T = d_{F} V g - d_{A} V g$
From sphere B: $T = d_{B} V g - d_{F} V g$
Equating the two expressions for tension: $d_{F} V g - d_{A} V g = d_{B} V g - d_{F} V g$
Cancel $V g$ from all terms: $d_{F} - d_{A} = d_{B} - d_{F}$
Rearranging: $2 d_{F} = d_{A} + d_{B}$
So, $d_{A} + d_{B} = 2 d_{F}$ .

Step 4: Check the Conditions
From the analysis:

For sphere A (top): $d_{A} < d_{F}$ must be true.
For sphere B (bottom): $d_{B} > d_{F}$ must be true.
And the density relation: $d_{A} + d_{B} = 2 d_{F}$ must hold.

Final Answer: The arrangement is possible only if $d_{A} + d_{B} = 2 d_{F}$ , $d_{A} < d_{F}$ , and $d_{B} > d_{F}$ . Among the options, $d_{A} + d_{B} = 2 d_{F}$ is correct and necessary.

Detailed Solution

Related Topics and Formulae

Detailed Solution

Related Topics and Formulae

Student who searched for similar questions

Questions 1

Questions 2

Questions 3

Questions 4

Questions 5