A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density \sigma at equilibrium position. The extension x0 of the spring when it is in equilibrium is : (Here k is spring constant)

Engineering

Physics

Equilibrium

SHM of Spring Block System

Buoyancy

Question

A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density $σ$ at equilibrium position. The extension x₀ of the spring when it is in equilibrium is :

(Here k is spring constant)

$\frac{Mg}{k}$

$\frac{Mg}{k} (1 - \frac{LAσ}{2 M})$

$\frac{Mg}{k} (1 - \frac{LAσ}{M})$

$\frac{Mg}{k} (1 + \frac{LAσ}{M})$

$Mg = {kx}_{0} + \frac{σAL}{2} g$

$\Rightarrow x_{0} = \frac{Mg}{k} (1 - \frac{LAσ}{2 M})$

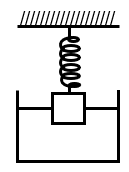
This problem involves a cylinder suspended by a spring and partially submerged in a liquid. At equilibrium, the forces acting on the cylinder are balanced. Let's analyze these forces step by step.

Step 1: Identify the forces acting on the cylinder at equilibrium.

Three forces act on the cylinder:

Weight (W): Acts downward. $W = M g$
Spring Force (F_spring): Acts upward. According to Hooke's Law, $F_{s p r i n g} = k x_{0}$ , where $x_{0}$ is the extension of the spring at equilibrium.
Buoyant Force (F_B): Acts upward. According to Archimedes' principle, the buoyant force is equal to the weight of the liquid displaced. The cylinder is half submerged, so the volume of liquid displaced is $\frac{V}{2}$ . The total volume of the cylinder is $V = A L$ . Therefore, the buoyant force is $F_{B} = (\frac{V}{2}) σ g = (\frac{A L}{2}) σ g$ .

Step 2: Apply the condition for equilibrium.

For the cylinder to be in equilibrium, the net force on it must be zero. The two upward forces (spring and buoyancy) must balance the downward force (weight).

Therefore, we can write the force balance equation:

k x_{0} + F_{B} = M g

Substituting the expression for $F_{B}$ :

k x_{0} + (\frac{A L σ g}{2}) = M g

Step 3: Solve for the extension $x_{0}$ .

Rearrange the equation to isolate $x_{0}$ :

k x_{0} = M g - \frac{A L σ g}{2}

x_{0} = \frac{M g - \frac{A L σ g}{2}}{k}

Factor out $M g$ from the numerator:

x_{0} = \frac{M g (1 - \frac{A L σ}{2 M})}{k}

This simplifies to the final expression for the spring extension at equilibrium:

x_{0} = \frac{M g}{k} (1 - \frac{L A σ}{2 M})

Final Answer: Comparing this result with the given options, the correct one is:

$\frac{Mg}{k} (1 - \frac{L A σ}{2 M})$

Detailed Solution

Related Topics and Formulae

Detailed Solution

Related Topics and Formulae

Student who searched for similar questions

Questions 1

Questions 2

Questions 3

Questions 4

Questions 5