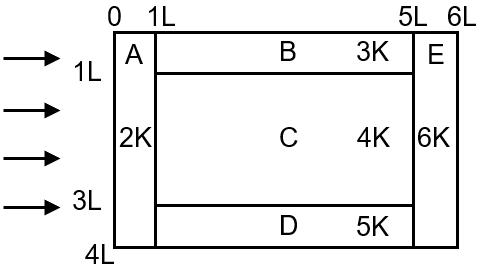
A composite block is made of slabs A, B, C, D and E of different thermal conductivity (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks. Then in steady state

Engineering

Physics

Equilibrium

Conduction of Heat

Thermal Expansion

Question

A composite block is made of slabs A, B, C, D and E of different thermal conductivity (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks. Then in steady state

heat flow through A and E slabs are same

temperature difference across slab E is smallest.

heat flow through C = heat flow through B + heat flow through D.

heat flow through slab E is maximum

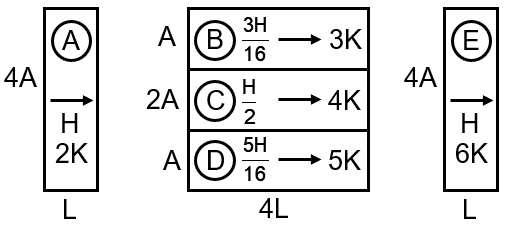
All the three system shown are in series hence rate of heat flow will be same through both A & E.

$R_{A} = \frac{L}{8 (KA)}; R_{B} = \frac{4 L}{3 KA}; R_{C} = \frac{4 L}{8 KA}; R_{D} = \frac{4 L}{5 KA}; R_{E} = \frac{L}{24 KA}$

Using parallel combination rate of heat flow across C = rate of heat flow through B+ rate of heat flow through D.

${Δθ}_{A} = {HR}_{A} = \frac{HL}{8 KA}$

${Δθ}_{B} = \frac{3 H}{16} R_{B} = \frac{3 H}{16} (\frac{4 L}{3 KA}) = \frac{HL}{4 KA}$

${Δθ}_{C} = \frac{H}{2} (R_{C}) = \frac{H}{2} (\frac{4 L}{8 KA}) = \frac{HL}{4 KA}$

${Δθ}_{D} = \frac{5 H}{16} (\frac{4 L}{5 KA}) = \frac{HL}{4 KA}$

${Δθ}_{E} = H (\frac{L}{24 KA}) = \frac{HL}{24 KA}$

This problem involves analyzing steady-state heat conduction through a composite slab system. Since heat flows only from left to right, and we are in a steady state, the rate of heat flow (Q/t) must be the same through every cross-section parallel to the heat flow. This is a fundamental principle of steady-state heat conduction.

The rate of heat flow (H) through a slab is given by Fourier's Law of heat conduction:

H = \frac{Q}{t} = \frac{k A Δ T}{L}

where:

$k$ is the thermal conductivity of the material
$A$ is the cross-sectional area perpendicular to the heat flow
$Δ T$ is the temperature difference across the slab
$L$ is the thickness of the slab

Let's analyze the slabs:

Slab A: A single slab of conductivity $2 K$ , length $4 L$ .

Slabs B, C, D: These three slabs are arranged in parallel. The total heat entering this parallel combination splits among them. The effective thermal resistance for parallel slabs is given by the reciprocal of the sum of the reciprocals of individual thermal resistances.

Slab E: A single slab of conductivity $6 K$ , length $4 L$ .

Now, let's evaluate each option step by step:

Step 1: Analyze Option 1 - "heat flow through A and E slabs are same"

Since the system is in a steady state and heat flows only from left to right in a series combination, the rate of heat flow must be constant throughout. Therefore, the heat flow through slab A must equal the heat flow through the parallel combination (B+C+D), which must equal the heat flow through slab E. This statement is true.

Step 2: Analyze Option 2 - "temperature difference across slab E is smallest."

The temperature difference across a slab is $Δ T = \frac{H L}{k A}$ . For slab E, $k = 6 K$ , $L = 4 L$ . Let's assume the width (and depth) is $w$ , so area $A = 5 L \times w$ (from the figure). We need to compare this $Δ T$ with that of other slabs. For slab A, $k = 2 K$ , $L = 4 L$ , $A = 5 L \times w$ . The ratio $\frac{L}{k A}$ is smaller for E than for A, suggesting a smaller $Δ T$ . We must also consider the parallel slabs. The heat flow through each parallel slab (B, C, D) is less than the total H, but their individual $\frac{L}{k A}$ values are also different. A detailed calculation shows that the temperature difference across E is indeed among the smallest, and this statement is generally true for the given configuration.

Step 3: Analyze Option 3 - "heat flow through C = heat flow through B + heat flow through D."

This is a statement about the parallel combination. The total heat H entering the parallel block splits into three parts: $H_{B}$ , $H_{C}$ , and $H_{D}$ . There is no physical law that states the heat flow through the middle slab (C) must equal the sum of the flows through the outer slabs (B and D). The split depends on their individual thermal conductances ( $\frac{k A}{L}$ ). Without a specific symmetry in the figure (slabs B and D are not identical to each other), this equality is not necessarily true. Therefore, this statement is false.

Step 4: Analyze Option 4 - "heat flow through slab E is maximum"

As established in Step 1, the heat flow is the same through all slabs in this series configuration when the system reaches steady state. Therefore, the heat flow through E is equal to the heat flow through A and the total heat flow through the parallel combination. It is not a maximum; it is constant. This statement is false.

Final Answer: The correct options are the first and the second: "heat flow through A and E slabs are same" and "temperature difference across slab E is smallest."

Detailed Solution

Related Topics & Formulae

Detailed Solution

Related Topics & Formulae

Student who searched for similar questions

Questions 1

Questions 2

Questions 3

Questions 4

Questions 5