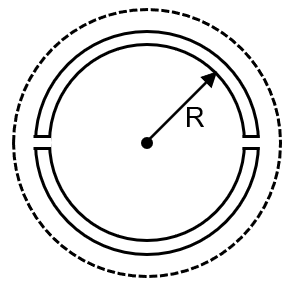
A wooden wheel of radius R is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross sectional area S and length L. L is slightly less than 2πR. To fit the ring on the wheel, it is heated so that its temperature rises by ΔT and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is α, and its Young's modulus is Y, the force that one part of the wheel applies on the other part is :
Thermal stress = YT
Force developed = YST

This problem involves thermal expansion, elasticity, and force calculation. Let's break it down step by step.
Step 1: Understanding the Ring's Expansion
The metal ring is heated so its temperature rises by ΔT. Its length increases due to thermal expansion. The original length is L (which is slightly less than 2πR). The change in length (ΔL) due to heating is given by the formula for linear expansion:
Since L is very close to 2πR, we can approximate L ≈ 2πR. So,
This ΔL is the extra length that allows the ring to just slip over the wheel.
Step 2: Understanding the Cooling and Stress
After the ring cools back to the original temperature, it tries to contract to its original length L. But since it is now around the wheel (which has circumference 2πR, slightly larger than L), the ring cannot contract fully. This causes a strain in the ring.
The attempted contraction is ΔL (the same as the expansion we calculated). However, the ring is constrained by the wheel, so the actual change in length is prevented. Therefore, the strain (ε) in the ring is:
So, the strain is approximately αΔT.
Step 3: Relating Strain to Stress and Force
Young's modulus (Y) is defined as stress (σ) divided by strain (ε):
Therefore, the stress in the ring is:
Stress is force per unit area. The cross-sectional area of the ring is S. Therefore, the tension force (T) in the ring is:
Step 4: Relating Ring Tension to the Force on the Wheel Parts
The ring is circular and applies an inward force all around its circumference. This inward force is what holds the two semicircular parts of the wheel together.
For a circular ring under uniform tension T, the total inward force it exerts on whatever is inside it is the same all around. However, the question asks for the force that one part of the wheel applies on the other part. This is essentially the force required to hold the two halves together, which is provided by the ring.
Imagine the ring pressing inward. The force from the ring on the wheel is distributed. But to find the force between the two wheel parts, we can think about the equilibrium of one semicircular part.
The tension T in the ring acts tangentially. For a semicircular part, the vertical components of the tension from the ring cancel out, but the horizontal components add up. The total compressive force (F) that the ring exerts on one semicircular part, pushing it towards the other part, is actually 2T. This is a standard result for the force from a tight string or ring on a curved surface.
Therefore, the force F that one part of the wheel applies on the other part is equal and opposite to this compressive force from the ring:
Final Answer: The force is
Thermal Expansion: The change in length of a material when heated. ΔL = L₀ α ΔT, where α is the coefficient of linear expansion.
Young's Modulus: A measure of the stiffness of a material. Y = Stress / Strain = (F/A) / (ΔL/L).
Stress and Strain: Stress (σ) is force per unit area. Strain (ε) is the ratio of change in length to original length.
Force in a Circular Ring: The total inward force exerted by a ring under uniform tension T on its contents is 2T. This is derived from integrating the components of the tension force around the semicircle.