A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is µ and tan θ > µ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1 = mg (sin θ – µ cos θ) to P2 = mg(sin θ + µ cos ), the frictional force f versus P graph will look like
Tanθµ
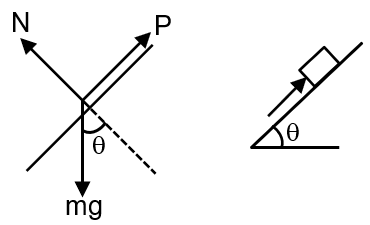
force for which f = 0 P0 = mg sin
Case I P = mg (sin – µ cos ) P < P0
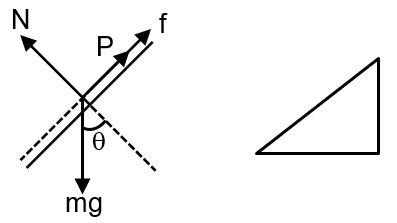
P + f = mg sin
mg (sinq – µcos) + f = mg sin
f = µ mgcos
Case II P = mg (sin + µ cos) > P0
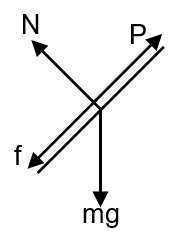
P = f + mg sinq
mg (sinq + µ cos) = f + mg sin
f = µ mg cos]
This problem involves analyzing the frictional force acting on a block held stationary on an inclined plane by an external force P. The key is to understand how the frictional force (f) changes as the applied force (P) is varied. Let's break it down step by step.
Step 1: Understand the Forces
The forces acting on the block parallel to the inclined plane are:
Since the block is held stationary, the net force parallel to the plane is zero.
Step 2: Direction of Friction
The direction of friction depends on the value of P relative to the gravitational component.
Step 3: Equation for Equilibrium
For the block to be stationary, the sum of forces parallel to the plane is zero. We consider two cases based on the direction of friction:
Case 1: Friction acting up the plane (f positive)
This happens when P is relatively small. The equilibrium equation is:
So,
Here, f is static friction and can vary from 0 to its maximum value . This case is valid as long as and P is between and .
Case 2: Friction acting down the plane (f negative)
This happens when P is relatively large. The equilibrium equation is:
So,
Here, f is negative (since it acts down the plane) and its magnitude can vary from 0 to . This case is valid for P between and .
Step 4: Analyze the f vs P graph
From the equations:
However, the friction has a limit: . So the graph is V-shaped but with the tips cut off at the maximum friction values. The minimum P for which the block can be held stationary is (friction at its maximum up the plane) and the maximum P is (friction at its maximum down the plane). At , the friction is zero.
Final Answer: The f vs P graph is a V-shaped graph with its vertex at (P = mg sinθ, f = 0). The arms of the V have slopes of -1 and +1, but they are truncated at f = ±μmg cosθ. Therefore, the correct graph is the one that looks like an inverted 'V' with horizontal lines at the top and bottom, representing the maximum static friction limits.
Related Topics and Formulae
Friction on an Inclined Plane: The maximum static friction force is given by , where N is the normal force.
Equilibrium Condition: For an object to be stationary, the net force in any direction must be zero. Here, we resolved forces parallel to the inclined plane.
Graph Interpretation: The f vs P graph is piecewise linear with slopes determined by the equilibrium equations, and it is bounded by the maximum friction value.