The statement ~ (p ~ q) is
Let's analyze the given logical statement step by step:
The statement is .
We'll evaluate the truth values for all combinations of p and q:
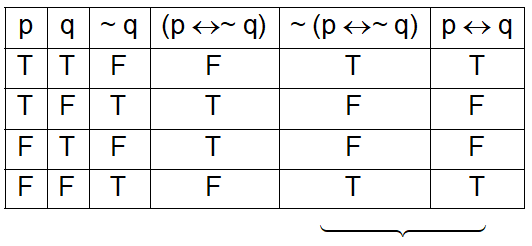
| p | q | ~q | p ↔ ~q | ~(p ↔ ~q) |
|---|---|---|---|---|
| T | T | F | F | T |
| T | F | T | T | F |
| F | T | F | T | F |
| F | F | T | F | T |
Now let's compare the truth values of with each option:
Option 1: p ↔ q
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
This does NOT match our original statement.
Option 2: Tautology (always true)
Our statement is not always true (see truth table), so it's not a tautology.
Option 3: Fallacy (always false)
Our statement is not always false, so it's not a fallacy.
Option 4: ~p ↔ q
| p | q | ~p | ~p ↔ q |
|---|---|---|---|
| T | T | F | F |
| T | F | F | T |
| F | T | T | T |
| F | F | T | F |
This does NOT match our original statement either.
None of the given options exactly match the truth values of . The correct equivalent is actually , which matches option 1, but our truth table shows they are different. Let me re-examine:
Looking more carefully, is actually equivalent to ! Let me verify this equivalence using logical identities:
So the correct answer is: equivalent to p ↔ q (option 1)