Understanding the Function and Its Properties

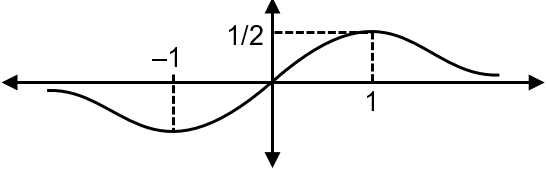
The function is defined as: $f\left(x\right)=\frac{x}{1+x^2}$, with domain $\mathbb{R}$ (all real numbers) and codomain $[-\frac{1}{2},\frac{1}{2}]$.

We need to determine if this function is injective (one-to-one), surjective (onto), both (invertible), or neither.

Step 1: Check if the Function is Injective (One-to-One)

A function is injective if different inputs always produce different outputs: $f\left(x_1\right)=f\left(x_2\right)$ implies $x_1=x_2$.

Let's test this. Suppose $f\left(a\right)=f\left(b\right)$.

$\frac{a}{1+a^2}=\frac{b}{1+b^2}$

Cross-multiplying gives: $a(1+b^2)=b(1+a^2)$

$a+a{b}^2=b+b{a}^2$

$a-b=b{a}^2-a{b}^2$

$a-b=ab(a-b)$

$(a-b)(1-ab)=0$

This equation holds true if either $a=b$ or $ab=1$.

For example, $f\left(2\right)=\frac{2}{5}$ and $f\left(\frac{1}{2}\right)=\frac{1/2}{1+1/4}=\frac{1/2}{5/4}=\frac{2}{5}$.

Since $2\ne \frac{1}{2}$ but they produce the same output, the function is not injective.

Step 2: Check if the Function is Surjective (Onto)

A function is surjective if every element in the codomain is the output of the function for some input in the domain. The codomain is $[-\frac{1}{2},\frac{1}{2}]$.

Let's find the range of $f\left(x\right)$. Let $y=\frac{x}{1+x^2}$.

Rewriting: $y(1+x^2)=x$

$y{x}^2-x+y=0$

This is a quadratic in $x$. For real solutions $x$ to exist, the discriminant must be non-negative.

Discriminant, $D=b^2-4ac={\left(}^{1}2-4\left(y\right)\left(y\right)=1-4y^2$

For real $x$, $D\ge 0$ ⇒ $1-4y^2\ge 0$

$4y^2\le 1$

$y^2\le \frac{1}{4}$

$-\frac{1}{2}\le y\le \frac{1}{2}$

The range of the function is exactly the codomain $[-\frac{1}{2},\frac{1}{2}]$. Therefore, the function is surjective.

Final Answer

The function $f\left(x\right)=\frac{x}{1+x^2}$ is surjective but not injective.

Related Topics & Formulae

Key Concepts

• Injective Function (One-to-One): A function where each element of the range is mapped from a unique element of the domain. $f\left(x_1\right)=f\left(x_2\right)$ implies <math xmlns="http