Let a function f : (0, ) → (0, ) be defined by f(x) = . Then f is:
x > 0
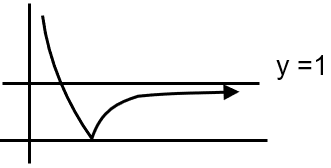
⇒ f (x) is one-one but not onto
Let's analyze the function f: (0, ∞) → (0, ∞) defined by f(x) = |1 - 1/x|.
Since x > 0, we can analyze the expression inside the absolute value.
For x > 0:
So, we can write f(x) as a piecewise function:
A function is injective if f(a) = f(b) implies a = b.
Let's test with specific values. Consider x₁ = 1/2 and x₂ = 2.
For x₁ = 1/2 (which is < 1): f(1/2) = 1/(1/2) - 1 = 2 - 1 = 1.
For x₂ = 2 (which is ≥ 1): f(2) = 1 - 1/2 = 1/2.
These are different. Let's try to find two different inputs that give the same output.
Suppose f(a) = f(b) = k, where k is some positive number.
Case 1: If both a and b are in (0,1), then f(a)=1/a - 1 = k and f(b)=1/b - 1 = k. This implies 1/a = 1/b, so a = b.
Case 2: If both a and b are in [1, ∞), then f(a)=1 - 1/a = k and f(b)=1 - 1/b = k. This implies 1/a = 1/b, so a = b.
Case 3: The interesting case is if one input is in (0,1) and the other is in [1, ∞).
Let a ∈ (0,1) and b ∈ [1, ∞). Then f(a) = 1/a - 1 and f(b) = 1 - 1/b.
Set them equal: 1/a - 1 = 1 - 1/b
Simplify: 1/a + 1/b = 2
Multiply both sides by ab: b + a = 2ab
Rearrange: 2ab - a - b = 0
We can rewrite this as: 4ab - 2a - 2b = 0
Add 1 to both sides: 4ab - 2a - 2b + 1 = 1
This factors as: (2a - 1)(2b - 1) = 1
For example, let 2a - 1 = 2 and 2b - 1 = 1/2. Then a = 3/2 and b = 3/4. But note, a must be in (0,1) and b in [1, ∞). Here, a=1.5 (not < 1) and b=0.75 (not ≥ 1). This doesn't satisfy our initial conditions.
Let's try a specific pair. Let a = 1/3 and solve for b from the equation 1/a + 1/b = 2.
1/(1/3) + 1/b = 2 → 3 + 1/b = 2 → 1/b = -1 → b = -1. But b must be positive. This is impossible.
Let's try a value closer to 1. Let a = 2/3. Then 1/(2/3) + 1/b = 2 → 3/2 + 1/b = 2 → 1/b = 1/2 → b = 2.
Now, check if f(a) = f(b). a=2/3 is in (0,1), b=2 is in [1, ∞).
f(2/3) = 1/(2/3) - 1 = 3/2 - 1 = 1/2.
f(2) = 1 - 1/2 = 1/2.
So, f(2/3) = f(2) = 1/2, but 2/3 ≠ 2. Therefore, the function is not injective.
A function is surjective if for every y in the codomain (0, ∞), there exists an x in the domain (0, ∞) such that f(x) = y.
Let y be any positive number, y > 0.
We need to solve f(x) = y.
Look at the piecewise definition:
For x ∈ (0,1): f(x) = 1/x - 1 = y → 1/x = y + 1 → x = 1/(y+1).
Since y > 0, y+1 > 1, so x = 1/(y+1) is in (0,1). This is valid.
For x ∈ [1, ∞): f(x) = 1 - 1/x = y → 1/x = 1 - y → x = 1/(1-y).
For this to be valid, we need 1-y > 0 (so that x > 0) and also x = 1/(1-y) ≥ 1 (since we are in the x≥1 branch).
The condition x ≥ 1 implies 1/(1-y) ≥ 1. Since 1-y > 0, we can multiply both sides by (1-y): 1 ≥ 1-y → y ≥ 0. This is already true.
But we also need 1-y > 0, which means y < 1.
So, for any y in the codomain:
Therefore, for every y > 0, there exists at least one x > 0 such that f(x)=y. The function is surjective.
The function f is not injective (as shown by f(2/3)=f(2)=1/2) but it is surjective.
Therefore, the correct option is: not injective but it is surjective.
Injective Function (One-to-One): A function f: A → B is injective if different elements of A always map to different elements of B. Formally: if f(a) = f(b) then a = b.
Surjective Function (Onto): A function f: A → B is surjective if every element of B is the image of at least one element of A. Formally: for every b in B, there exists an a in A such that f(a)=b.
Absolute Value Function: |a| = a if a ≥ 0, and |a| = -a if a < 0.
Solving Equations with Absolute Value: Often requires considering cases based on the sign of the expression inside the absolute value.