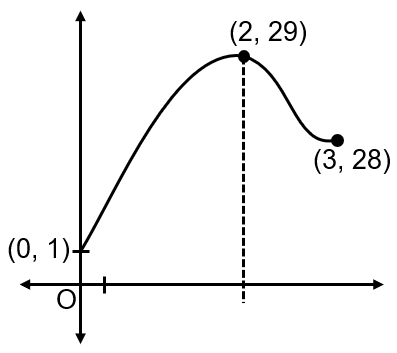
The function f : [0, 3] [1, 29], defined by f(x) = 2x3 – 15x2 + 36x + 1, is
f(x) = 2x3 – 15x2 + 36x + 1
f '(x) = 6x2 – 30x + 36 = 6 (x – 2) (x – 3)
![]()
sign of f ' changes in [0 3]
function is not one‑one
f(0) = 1 ; f(2) = 29 and f(3) = 28
Range = [1, 29]
Function is onto but not one‑one.
The function is defined as , with domain and codomain . We need to determine if it is one-one (injective) and/or onto (surjective).
A function is one-one if every element in the domain maps to a unique element in the codomain. For a continuous function on a closed interval, we can check its monotonicity by finding its derivative.
First, find the derivative: .
Set the derivative to zero to find critical points: .
Divide by 6: .
Factor: , so critical points are at and .
Now, test the sign of in the intervals determined by the critical points within the domain [0, 3]:
Since the function increases on [0, 2) and decreases on (2, 3], it is not strictly monotonic over the entire domain. Therefore, it is not one-one. For example, different x-values (like near 0 and near 3) can produce the same f(x) value.
A function is onto if every element in the codomain [1, 29] is the image of at least one element in the domain [0, 3]. We can check this by finding the range of f(x) on [0, 3].
Evaluate f(x) at the endpoints and critical points:
The minimum value is 1 (at x=0) and the maximum value is 29 (at x=2). Since f(x) is continuous, by the Intermediate Value Theorem, it takes every value between 1 and 29. The codomain is exactly [1, 29], which matches the range. Therefore, the function is onto.
The function is onto but not one-one.