Let X be a set with exactly 5 elements and Y be a set with exactly 7 elements. If α is the number of one-one functions from X to Y and β is the number of onto functions from Y to X, then the value of \frac{1}{5 !} (β

Engineering

Mathematics

Classification of Functions

Question

Let X be a set with exactly 5 elements and Y be a set with exactly 7 elements. If α is the number of one-one functions from X to Y and β is the number of onto functions from Y to X, then the value of $\frac{1}{5!}$ (β – α) is______.

$7 = [\begin{array}{l} 1, 1, 1, 1, 3 \\ 1, 1, 1, 2, 2 \end{array}$

$β = (\frac{7!}{4! \cdot 3!} + \frac{7!}{3! \cdot (2!) \cdot 2!}) \times 5! = (\frac{7 \cdot 6 \cdot 5}{3} + \frac{7 \cdot 6 \cdot 5 \cdot 4}{8}) \cdot 5!$

$= 35 \times 4 \times 5! = \frac{7 \cdot 5 \cdot 4 \cdot 3}{3} \times 5! = \frac{10}{3} \times 7!$

$∴ β - α (\frac{10}{3} \times 7 \cdot 6 - \frac{7 \cdot 6}{2}) . 5! \Rightarrow \frac{1}{5!} (β - α) = 119 .00$

Understanding the Problem

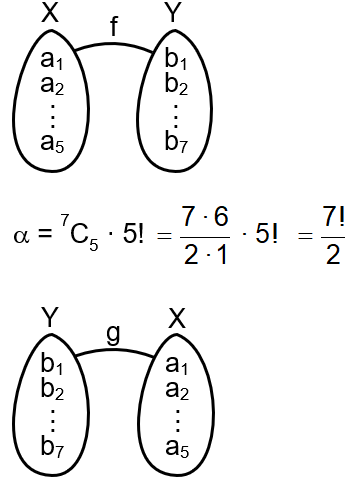
We are given two sets: X with 5 elements and Y with 7 elements. We need to find:

α: the number of one-one (injective) functions from X to Y.
β: the number of onto (surjective) functions from Y to X.
Then compute $\frac{1}{5!}$ (β - α).

Step 1: Find α (Number of One-One Functions from X to Y)

A one-one function means each element in X maps to a distinct element in Y. Since |X| = 5 and |Y| = 7, we have enough elements in Y to assign distinct images.

The number of one-one functions from a set of size m to a set of size n (where n ≥ m) is given by the permutation formula: P(n, m) = n! / (n - m)!.

So, for X to Y: m = 5, n = 7.

α = P(7, 5) = 7! / (7 - 5)! = 7! / 2!.

Let's compute the value:

7! = 5040, 2! = 2, so α = 5040 / 2 = 2520.

Step 2: Find β (Number of Onto Functions from Y to X)

An onto function means every element in X has at least one pre-image in Y. Here, we are mapping from Y (size 7) to X (size 5).

The number of onto functions from a set of size n to a set of size m is given by the inclusion-exclusion principle:

β = \sum_{k = 0}^{m} {(-1)}^{k} (\binom{m}{k}) {(m - k)}^{n}

Where n = 7 (size of Y) and m = 5 (size of X).

So, β = $\sum_{k = 0}^{5} {(-1)}^{k} (\binom{5}{k}) {(5 - k)}^{7}$

Let's compute each term:

For k=0: ${(-1)}^{0} (\binom{5}{0}) 5^{7} = 1 \times 1 \times 78125 = 78125$
For k=1: ${(-1)}^{1} (\binom{5}{1}) 4^{7} = - 1 \times 5 \times 16384 = - 81920$
For k=2: ${(-1)}^{2} (\binom{5}{2}) 3^{7} = 1 \times 10 \times 2187 = 21870$
For k=3: ${(-1)}^{3} (\binom{5}{3}) 2^{7} = - 1 \times 10 \times 128 = - 1280$
For k=4: ${(-1)}^{4} (\binom{5}{4}) 1^{7} = 1 \times 5 \times 1 = 5$
For k=5: ${(-1)}^{5} (\binom{5}{5}) 0^{7} = - 1 \times 1 \times 0 = 0$

Now, sum these values: 78125 - 81920 + 21870 - 1280 + 5 + 0.

Let's calculate step by step:

78125 - 81920 = -3795

-3795 + 21870 = 18075

18075 - 1280 = 16795

16795 + 5 = 16800

So, β = 16800.

Step 3: Compute the Expression $\frac{1}{5!}$ (β - α)

We have:

α = 2520

β = 16800

5! = 120

First, compute β - α = 16800 - 2520 = 14280.

Now, compute $\frac{1}{120}$ × 14280 = 14280 / 120.

14280 ÷ 120 = 119.

Final Answer

The value of $\frac{1}{5!}$ (β - α) is 119.

Key Formulae

Number of one-one functions from a set of size m to a set of size n (n ≥ m): $P (n, m) = \frac{n!}{(n - m)!}$
Number of onto functions from a set of size n to a set of size m: $\sum_{k = 0}^{m} {(-1)}^{k} (\binom{m}{k}) {(m - k)}^{n}$

Detailed Solution

Understanding the Problem

Step 1: Find α (Number of One-One Functions from X to Y)

Step 2: Find β (Number of Onto Functions from Y to X)

Step 3: Compute the Expression $\frac{1}{5!}$ (β - α)

Final Answer

Related Topics

Key Formulae

Detailed Solution

Understanding the Problem

Step 1: Find α (Number of One-One Functions from X to Y)

Step 2: Find β (Number of Onto Functions from Y to X)

Step 3: Compute the Expression 15!(β - α)

Final Answer

Related Topics

Key Formulae

Student who searched for similar questions

Questions 1

Questions 2

Questions 3

Questions 4

Questions 5

Step 3: Compute the Expression $\frac{1}{5!}$ (β - α)