The equation of the circle passing through the foci of the ellipse and having centre at (0, 3) is :
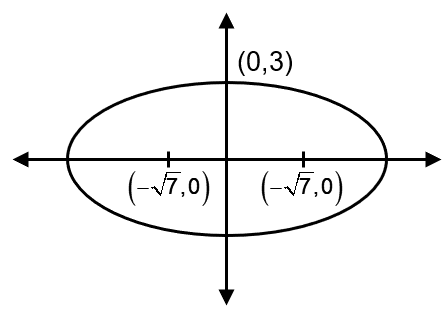
r2 = 7 + 9
r2 = 16
r = 4
(x – 0)2 + (y – 3)2 = 16
x2 + y2 – 6y – 7 = 0.
We are given an ellipse equation: . We need to find the equation of a circle that passes through the ellipse's foci and has its center at (0, 3).
The standard form of an ellipse is , where .
Comparing with the given equation: and . Therefore, and .
The distance from the center to a focus, , is given by .
Substituting the values: .
Since the major axis is along the x-axis, the coordinates of the foci are = .
So, the two foci are: F1 = and F2 = .
The circle has its center at (0, 3). The general equation of a circle with center (h, k) and radius r is:
.
For center (0, 3), we have and . This gives and .
Substituting these values, the equation becomes: .
Simplifying: .
Our goal is to find the value of the constant .
Since the circle passes through both foci, the coordinates of each focus must satisfy the circle's equation. We can use either focus to find .
Let's use the focus F1 = .
Substitute x = and y = 0 into the circle's equation:
This simplifies to:
Therefore, .
Substitute back into the general circle equation:
Which gives the final equation:
The equation of the circle is: x² + y² – 6y – 7 = 0
Standard Equation (Horizontal Major Axis): , where a > b.
Foci: Located at , where .
Standard Form:
Center: