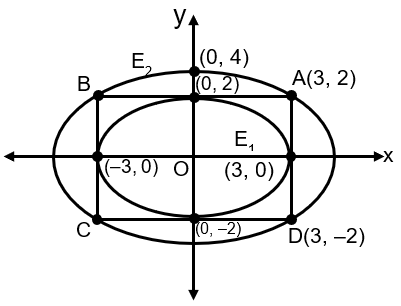
The ellipse E_{1} : \frac{x^{2}}{9} + \frac{y^{2}}{4}= 1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is

Engineering

Mathematics

Standard Ellipse

Question

The ellipse $E_{1} : \frac{x^{2}}{9} + \frac{y^{2}}{4}$ = 1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E₂ passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E₂ is

$\frac{3}{4}$

$\frac{1}{2}$

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{2}}{2}$

Equation of $E_{2} is \frac{x^{2}}{a^{2}} + \frac{y^{2}}{16} = 1$

Since E₂ passes through (3, 2)

$\Rightarrow \frac{9}{a^{2}} = \frac{3}{4} or a^{2} = 12$

$' e' or E_{2} = \sqrt{1 - \frac{12}{16}} = \frac{1}{2}$

'e' of E₂ = $\sqrt{1 - \frac{12}{16}} = \frac{1}{2}$ . Ans.

Understanding the Problem

We are given two ellipses:

Ellipse E₁: $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$
Ellipse E₂: An unknown ellipse that circumscribes the rectangle R (which inscribes E₁) and passes through the point (0,4).

Our goal is to find the eccentricity of ellipse E₂.

Step-by-Step Solution

Step 1: Find the Rectangle R that Inscribes E₁

The standard form of ellipse E₁ is $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ .

Comparing with the given equation, we find: $a^{2} = 9 \Rightarrow a = 3$ and $b^{2} = 4 \Rightarrow b = 2$ .

For an ellipse aligned with the axes, the rectangle that inscribes it has sides parallel to the axes and touches the ellipse at its vertices. The length of the rectangle is $2 a = 6$ and the width is $2 b = 4$ .

Therefore, the vertices of rectangle R are at: $(- 3, - 2)$ , $(3, - 2)$ , $(3, 2)$ , and $(- 3, 2)$ .

Step 2: General Equation for Ellipse E₂

Ellipse E₂ circumscribes rectangle R. Since R is symmetric about both axes, it is natural to assume that E₂ is also centered at the origin and has its axes aligned with the coordinate axes. Its general equation is: $\frac{x^{2}}{A^{2}} + \frac{y^{2}}{B^{2}} = 1$ where A and B are its semi-major and semi-minor axes (A > B for this problem, as we will see).

Step 3: Conditions for Ellipse E₂

We have two conditions to find A and B:

Circumscribes Rectangle R: The ellipse must pass through the vertices of R. The most "constraining" vertices for an ellipse centered at the origin are those along the axes, i.e., (±3, 0) and (0, ±2). However, since our ellipse is larger (it circumscribes R), it must pass through the corners of R, which are at (±3, ±2). Let's use the point (3, 2).
Substituting (3, 2) into the equation of E₂: $\frac{3^{2}}{A^{2}} + \frac{2^{2}}{B^{2}} = 1 \Rightarrow \frac{9}{A^{2}} + \frac{4}{B^{2}} = 1$
Let's call this Equation (1).
Passes through (0, 4): The point (0,4) lies on the ellipse.
Substituting (0, 4) into the equation of E₂: $\frac{0^{2}}{A^{2}} + \frac{4^{2}}{B^{2}} = 1 \Rightarrow \frac{16}{B^{2}} = 1 \Rightarrow B^{2} = 16$
Let's call this Equation (2).

Step 4: Solve for A and B

From Equation (2), we have found that $B^{2} = 16$ , so $B = 4$ .

Substitute $B^{2} = 16$ into Equation (1): $\frac{9}{A^{2}} + \frac{4}{16} = 1 \Rightarrow \frac{9}{A^{2}} + \frac{1}{4} = 1$

Now, solve for A²: $\frac{9}{A^{2}} = 1 - \frac{1}{4} \Rightarrow \frac{9}{A^{2}} = \frac{3}{4}$

Taking reciprocal: $\frac{A^{2}}{9} = \frac{4}{3} \Rightarrow A^{2} = 9 \times \frac{4}{3} \Rightarrow A^{2} = 12$

So, the semi-axes of E₂ are $A = \sqrt{12} = 2 \sqrt{3}$ and $B = 4$ .

Since B > A (4 > 2√3 ≈ 3.46), our initial assumption about which axis is major was incorrect. For ellipse E₂, the y-axis is the major axis.

Let's redefine for clarity:

Semi-major axis, $a = B = 4$
Semi-minor axis, $b = A = \sqrt{12} = 2 \sqrt{3}$

Step 5: Find the Eccentricity (e)

The formula for the eccentricity of an ellipse is: $e = \sqrt{1 - \frac{b^{2}}{a^{2}}}$ where a is the semi-major axis and b is the semi-minor axis. </

Detailed Solution

Understanding the Problem

Step-by-Step Solution

Step 1: Find the Rectangle R that Inscribes E1

Step 2: General Equation for Ellipse E2

Step 3: Conditions for Ellipse E2

Step 4: Solve for A and B

Step 5: Find the Eccentricity (e)

Student who searched for similar questions

Questions 1

Questions 2

Questions 3

Questions 4

Questions 5

Step 1: Find the Rectangle R that Inscribes E₁

Step 2: General Equation for Ellipse E₂

Step 3: Conditions for Ellipse E₂