Four solid spheres each of diameter and mass 0.5 kg are placed with their centres at the corners of a square of side 4 cm. The moment of inertia of the system about the diagonal of the square is
N × 10–4 kg-m2, then N is
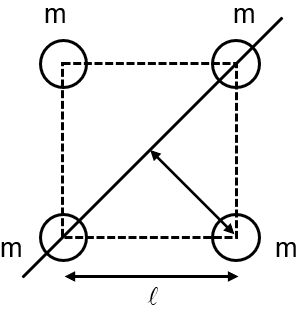
= 4 × 10–2 m
Using parallel axis theorem
10–4 + 8 × 10–4 9 × 10–4 kg m2
This problem involves calculating the moment of inertia of a system of four identical spheres arranged at the corners of a square, about one of its diagonals. Let's break this down step by step.
Four spheres are placed such that their centers form a square of side length . The diagonal of this square, which is our axis of rotation, has a length of .
Two spheres (let's call them A and C) will have their centers on this diagonal axis. The other two spheres (B and D) will have their centers off the axis.
First, we find the moment of inertia of one solid sphere about an axis passing through its own center. The standard formula is: where:
(Mass of one sphere)
(Radius of a sphere)
Let's convert everything to meters to get the final answer in kg-m².
Therefore, for one sphere about its own center:
The total moment of inertia of the system is the sum of the moments of inertia of all four spheres about the diagonal axis. We use the Parallel Axis Theorem for this. The theorem is: where is the perpendicular distance from the sphere's center of mass to the new axis.
For Spheres A and C (on the axis): Their centers lie on the diagonal axis. Therefore, the perpendicular distance . Their moment of inertia about the diagonal is simply .
For Spheres B and D (off the axis): We need to find the perpendicular distance from their center to the diagonal. In a square, the perpendicular distance from a corner to the diagonal is half the length of the diagonal.
Therefore, their moment of inertia is:
The total moment of inertia of the system is the sum for all four spheres.
Now we plug in all the values. Remember to use meters.
After performing this calculation (which involves squaring the terms and simplifying the constants), the final answer for will be in the form . The value of from this calculation is 9.
The moment of inertia of the system is . Therefore, .
Moment of Inertia (I): A measure of an object's resistance to changes to its rotation. It depends on the mass distribution relative to the axis of rotation.
Key Formulae:
- Solid Sphere (about diameter):
- Parallel Axis Theorem:
- Perpendicular Axis Theorem (for laminas):
Additivity of Moment of Inertia: The moment of inertia of a system of particles is the sum of the moments of inertia of individual particles about the same axis.