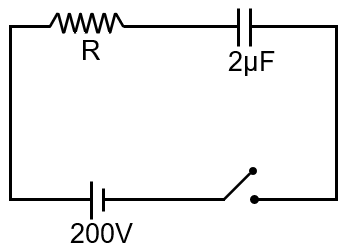
A resistor 'R' and 2µF capacitor in series is connected through a switch to 200V direct supply. Across the capacitor is a neon bulb that lights up at 120 V. Calculate the value of R to make the bulb light up 5s after the switch has been closed. (log10 2.5 = 0.4)
v = 200 (1 – e–t/t)
120 = 200(1 – e–t/t)
t/t = log(2.5) = 0.4
5 = (0.4) × R × 2 × 10–6
= R = 2.7 × 106
This problem involves an RC circuit where a resistor (R) and capacitor (2μF) are connected in series to a 200V DC supply. A neon bulb, connected across the capacitor, lights up when the capacitor voltage reaches 120V. We need to find the value of R such that this happens 5 seconds after closing the switch. The hint given is log₁₀(2.5) = 0.4.
Step 1: Understand the Charging Process
When the switch is closed, the capacitor starts charging through the resistor. The voltage across the capacitor (VC) at any time 't' is given by the charging equation:
Where:
Step 2: Plug in the Known Values
Substitute the known values into the equation:
Step 3: Solve for the Exponential Term
First, simplify the equation:
Now, rearrange to isolate the exponential term:
Step 4: Take Natural Logarithm (ln) on Both Sides
To solve for the exponent, we take the natural logarithm:
We know that ln(0.4) = -ln(2.5) because 1/0.4 = 2.5. Therefore:
The negative signs cancel out:
Step 5: Use the Given Logarithmic Value
The problem gives log₁₀(2.5) = 0.4. We need to convert this to a natural logarithm (ln). The conversion is: ln(x) = 2.3026 × log₁₀(x).
So our equation becomes:
Step 6: Solve for R
Rearrange the equation to solve for R:
First, calculate the denominator:
Now, calculate R:
This is approximately 2.7 × 10⁶ Ω.
Final Answer: The value of R is
RC Circuits: An RC circuit is composed of resistors and capacitors. The time constant (τ = R×C) determines how quickly the capacitor charges or discharges.
Capacitor Charging Equation: The voltage across a charging capacitor at time 't' is given by , where E is the source voltage.
Logarithmic Relationships: Solving exponential equations often requires using natural logarithms (ln) or common logarithms (log₁₀), with the conversion ln(x) ≈ 2.3026 × log₁₀(x).