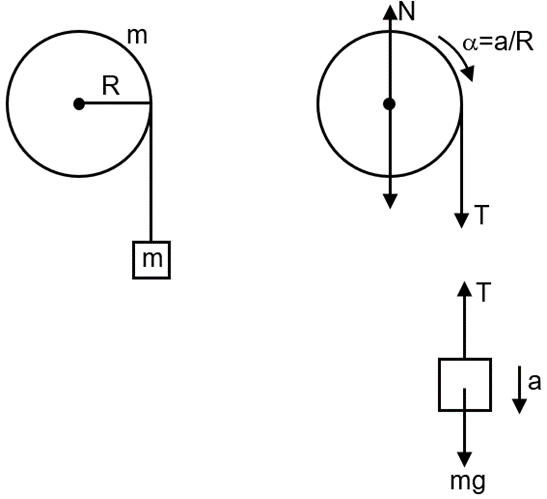
This problem involves a mass-pulley system where both the hanging mass and the pulley have mass m. The pulley is a uniform disc of radius R. We need to find the acceleration of the mass m when the string does not slip on the pulley.

Step 1: Identify the forces and set up equations

For the hanging mass (m):

The forces acting on it are its weight (mg) downward and the tension (T) in the string upward. Applying Newton's second law:

$mg-T=ma$ (Equation 1)

where $a$ is the linear acceleration of the mass.

Step 2: Analyze the motion of the pulley

The string does not slip, meaning the pulley rotates. The tension T provides a torque ($\tau$) on the pulley. The torque is given by:

$\tau =T\times R$

This torque causes an angular acceleration ($\alpha$) in the pulley. The relationship between torque and angular acceleration is:

$\tau =I\alpha$ (Equation 2)

where $I$ is the moment of inertia of the pulley.

Step 3: Relate linear and angular motion

Since the string does not slip, the linear acceleration of the mass (and the string) is related to the angular acceleration of the pulley by:

$a=\alpha R$ (Equation 3)

Step 4: Find the moment of inertia

The pulley is a uniform circular disc with mass m and radius R. The moment of inertia of a disc about its central axis is:

$I=\frac{1}{2}m{R}^2$ (Equation 4)

Step 5: Combine the equations

Substitute Equation 4 into Equation 2:

$TR=\left(\frac{1}{2}m{R}^2\right)\alpha$

Substitute Equation 3 ($\alpha =\frac{a}{R}$) into the above equation:

$TR=\left(\frac{1}{2}m{R}^2\right)\left(\frac{a}{R}\right)$

Simplify by canceling one R:

$T=\frac{1}{2}ma$ (Equation 5)

Step 6: Solve for acceleration (a)

Substitute Equation 5 into Equation 1:

$mg-\left(\frac{1}{2}ma\right)=ma$

Divide both sides by m:

$g-\frac{1}{2}a=a$

Bring terms with 'a' to one side:

$g=a+\frac{1}{2}a$

$g=\frac{3}{2}a$

Therefore, the acceleration is:

$a=\frac{2}{3}g$

Final Answer: The acceleration of the mass m is $\frac{2}{3}g$.

Related Topics and Formulae

Newton's Second Law for Rotation: The net torque ($\tau$) on a rigid body is equal to the product of its moment of inertia (I) and its angular acceleration ($\alpha$). $\tau =I\alpha$

Moment of Inertia for a Uniform Disc: For a disc of mass M and radius R rotating about its central axis, $I=\frac{1}{2}M{R}^2$.

No-Slip Condition: When a string unwinds without slipping from a pulley, the linear acceleration of the string (a) is related to the angular acceleration of the pulley ($\alpha$) by $a=\alpha R$.