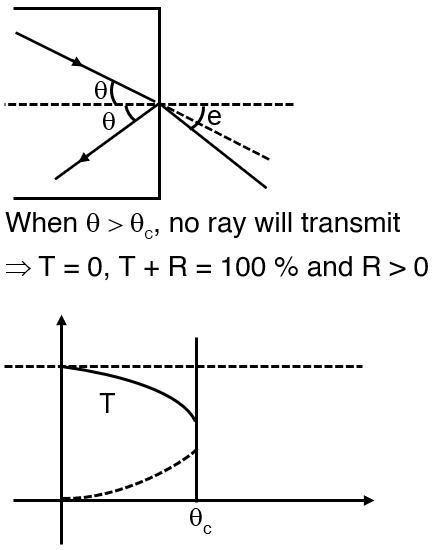
This question involves the behavior of light at an interface between two media (glass and air) and how the reflected (R) and transmitted (T) intensities change with the angle of incidence, θ. The key concept here is total internal reflection and the Fresnel equations.

When light travels from a denser medium (glass, with a higher refractive index, n_g) to a rarer medium (air, n_a ≈ 1), two important angles define its behavior:

1. Critical Angle (θ_c): This is the specific angle of incidence for which the angle of refraction becomes 90°. It is calculated using Snell's Law: $n_g\sin \left({\theta }_c\right)=n_a\sin (90°)$ Since sin(90°) = 1, the formula simplifies to: ${\theta }_c={\sin }^{-1}\left(\frac{n_a}{n_g}\right)$
2. Brewster's Angle (θ_B): This is the angle of incidence at which light with a particular polarization (parallel to the plane of incidence) is perfectly transmitted with zero reflection. It is given by: $\tan \left({\theta }_B\right)=\frac{n_a}{n_g}$

How Intensities Change with θ:

• For 0° ≤ θ < θ_c: Both reflection and transmission occur. The reflected intensity (R) is low but not zero at normal incidence (θ=0°) and increases gradually as θ increases. The transmitted intensity (T) is high at normal incidence and decreases gradually.
• At θ = θ_B: For one polarization component, the reflected intensity (R) drops to zero. The transmitted intensity (T) for that component is at a maximum. This causes a noticeable dip in the overall R vs. θ graph.
• At θ = θ_c: The angle of refraction is 90°, so the transmitted ray grazes along the interface. The transmitted intensity (T) becomes zero. The reflected intensity (R) becomes 100%.
• For θ > θ_c: Total internal reflection occurs. No light is transmitted into the air (T = 0). All incident light is reflected back into the glass (R = 100%).

Analyzing the Graphs: The correct sketch must show:

1. T starts at a high value at θ=0° and gradually decreases to zero at θ=θ_c. It remains zero for θ > θ_c.
2. R starts at a low value (not zero) at θ=0°, shows a dip at θ_B, increases to 100% at θ=θ_c, and remains at 100% for θ > θ_c.

The graph that matches this description is the one where the T curve falls smoothly to zero and the R curve has a distinct minimum (at Brewster's angle) before rising to 100% and staying there.

Related Topics & Formulae

Snell's Law: Governs refraction at an interface. $n_1\sin \left({\theta }_1\right)=n_2\sin \left({\theta }_2\right)$

Fresnel Equations: These are the precise formulas for calculating the reflection and transmission coefficients based on the angle of incidence and the polarization of light. They predict the Brewster's angle and the behavior of R and T.