The negation of ~ s (~ r s) is equivalent to
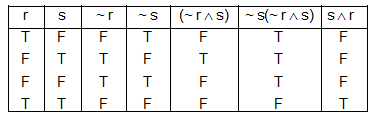
Negation of statement ~ s (~ r s) is equivalent to (s r)
We are asked to find the negation of the logical expression: ~ s ∨ (~ r ∧ s). We need to simplify this negation and find which of the given options it is equivalent to.
Original Expression:
Negation of the Expression:
De Morgan's Law states that the negation of a disjunction is the conjunction of the negations:
Applying this to our expression, where A is ¬s and B is (¬r ∧ s):
First, simplify ¬(¬s):
(The negation of a negation is the original proposition).
Now, simplify ¬(¬r ∧ s). We apply De Morgan's Law again, this time for a conjunction:
Applying this, where A is ¬r and B is s:
Now we substitute our simplifications back into the expression from Step 2:
We can now distribute s over the disjunction (r ∨ ¬s):
The term (s ∧ ¬s) is a contradiction. According to the Complement Law, a proposition AND its negation is always false:
Furthermore, anything OR False is just the original thing (Identity Law):
The negation of ~ s ∨ (~ r ∧ s) simplifies to .
Therefore, the correct equivalent expression from the options is:
Propositional Logic: The branch of logic that deals with propositions (statements that are either true or false) and their combinations using logical operators like AND (∧), OR (∨), and NOT (¬).
Logical Equivalence: Two compound propositions are logically equivalent if they have the same truth value for all possible combinations of truth values of their variables. The symbol ≡ is used to denote equivalence.
Simplification: The process of using logical equivalences to rewrite a complex proposition into a simpler, equivalent form. This is crucial for designing efficient digital circuits and constructing mathematical proofs.