Diameter of a plano - convex lens is 6 cm and thickness at the centre is 3 mm. If speed of light in material of lens is 2 × 108 m/s, the focal length of the lens is :
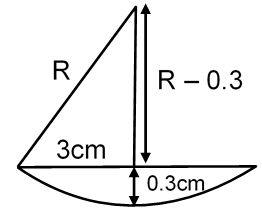
32 + (R – 0.3)2 = R2
32 + R2 – 0.6R + 0.09 = R2
To find the focal length of the plano-convex lens, we need to use the lens maker's formula. Let's break down the problem step by step.
Diameter of lens, D = 6 cm, so radius R = D/2 = 3 cm.
Thickness at center is small (3 mm) and can be ignored for thin lens approximation.
Speed of light in material, v = 2 × 108 m/s.
Speed of light in vacuum, c = 3 × 108 m/s.
Refractive index n = c / v
So, n = (3 × 108) / (2 × 108) = 1.5
For a thin lens:
For plano-convex lens: one side is flat (plane), so radius of curvature R1 = ∞ (infinity). The convex side has radius R2 = -R (by sign convention, if light comes from left, convex surface towards right has negative radius).
So, R1 = ∞, R2 = -3 cm.
Therefore, f = 6 cm? But wait, units: radius was in cm, so focal length f = 6 cm. However, options are in cm and 6 cm is not listed. Check sign convention.
Standard convention: For a plano-convex lens with convex side towards right, R1 = +∞ (for plane surface) and R2 = -R (since center of curvature is on the same side as incoming light).
So,
Given R = 3 cm, so , thus f = 6 cm. But 6 cm is not in options. Perhaps R is not 3 cm? Diameter is 6 cm, but for a plano-convex lens, the radius of curvature R is not necessarily half the diameter. Actually, the diameter given is likely the physical diameter, not the radius of curvature. We need to find R from geometry.
For a spherical surface, from geometry: , where t = thickness at center = 3 mm = 0.3 cm, D = 6 cm.
So,
Cancel R2:
So,
Since t << D, t2 is very small, neglect it:
So,
n = 1.5, R1 = ∞ (plane surface), R2 = -R = -15 cm (by convention).
So, focal length f = 30 cm.
The focal length of the lens is 30 cm.
Lens Maker's Formula: Used to calculate focal length based on refractive index and radii of curvature. For a thin lens:
Refractive Index: n = c / v, where c is speed in vacuum, v in medium.
Geometry of Spherical Surface: To find radius of curvature from chord length and sagitta (thickness): for small t.