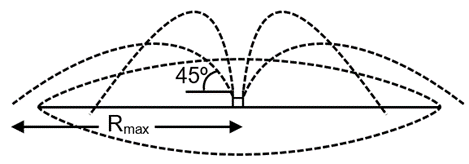
This question involves finding the total area around a fountain that gets wet when water is sprinkled in all directions with speed $v$. The water follows projectile motion trajectories, and the maximum range for a given speed occurs when the projection angle is 45°.

Step 1: Maximum Range of a Projectile
For a projectile launched with speed $v$ at an angle $\theta$, the range $R$ is given by: $R=\frac{v^2\sin 2\theta }{g}$ The maximum range, $R_{\text{max}}$, is achieved when $\sin 2\theta =1$ (i.e., $\theta =45°$). Therefore: $R_{\text{max}}=\frac{v^2}{g}$ This is the farthest distance from the fountain that a water droplet can reach.

Step 2: The Wet Area
Since the fountain sprinkles water in all directions (i.e., 360°), the area that gets wet is a circle. The radius of this circle is the maximum range, $R_{\text{max}}=\frac{v^2}{g}$. The area $A$ of a circle is given by: $A=\pi R^2$ Substituting the value of $R$: $A=\pi {\left(\frac{v^2}{g}\right)}^2=\pi \frac{v^4}{g^2}$

Final Answer: The total area around the fountain that gets wet is $\pi \frac{v^4}{g^2}$.

Related Topics and Formulae

Projectile Motion: The motion of an object under the influence of gravity only. Key equations include:

• Range: $R=\frac{v^2}{g}\sin 2\theta$
• Maximum Height: $H=\frac{v^2}{2g}{\sin }^2\theta$
• Time of Flight: $T=\frac{2v\sin \theta }{g}$

Area of a Circle: For a circle of radius $r$, the area is $A=\pi r^2$.