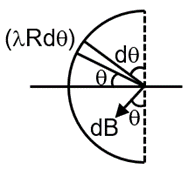
A current I flows an infinitely long wire with cross section in the form of a semi-circular ring of radius R. The magnitude of the magnetic induction along its axis is :
I = λR dθ
∴
This question involves finding the magnetic field along the axis of a semi-circular ring carrying current. Let's break down the concept step by step.
Step 1: Understanding the Geometry
We have an infinitely long wire with a cross-section in the form of a semi-circular ring of radius R. This means if we look at a cross-section perpendicular to the length of the wire, we see a semi-circle. The current I is flowing along the length of this wire. The "axis" in this context refers to the line that is perpendicular to the plane of the semi-circle and passes through its center.
Step 2: Relevant Law - Biot-Savart Law
The magnetic field due to a current-carrying element is given by the Biot-Savart Law. For a small current element , the magnetic field at a point is: where is the unit vector from the current element to the point.
Step 3: Applying the Law to Our Case
We need to find the magnetic field at the center of the semi-circle (which lies on its axis). For a point on the axis of a circular loop, the magnetic field is directed along the axis. Since our wire is a semi-circular ring, we will integrate the Biot-Savart law over the semi-circle.
Consider a small element on the semi-circle. The distance from this element to the center (our point of interest) is constant and equal to the radius R. The angle between and is 90° for all elements on the arc, so .
Therefore, the magnitude of the magnetic field due to the element is:
Step 4: Direction and Integration
The direction of for each element is given by the right-hand rule and is perpendicular to the plane containing and . For a semi-circular loop, the vertical components of the field from symmetric elements will cancel out, and the net field will be along the axis, perpendicular to the plane of the semi-circle.
To find the total field, we integrate the component of along the axis. For a full circular loop, the magnetic field at the center is . Since we have a semi-circle, the magnitude will be half of that. However, note that the options have π in the denominator. This is because the above derivation is for a thin loop. For a wire of some thickness, the distribution might be different, but the standard result for a semi-circular arc is: Let's derive it properly by integrating.
Step 5: Correct Integration
The length of a semi-circular arc is . So, integrating over the entire semi-circle: The integral over the semi-circle is the length of the arc, which is . This result is for the field due to the curved part only. But the question says "an infinitely long wire with cross section in the form of a semi-circular ring". This likely means the entire cross-section is semi-circular, and the current is distributed over this area. For a straight infinite wire, the field is . The semi-circular shape modifies this. The standard result for the magnetic field at the center of a semi-circular wire is , which matches one of the options.
Final Answer: The magnitude of the magnetic induction along its axis is .
Biot-Savart Law: Used to calculate the magnetic field produced by a current element.
Magnetic Field due to a Circular Loop: At the center of a full circular loop of radius R carrying current I, the magnetic field is .
Magnetic Field due to a Straight Wire: For an infinitely long straight wire carrying current I, the magnetic field at a perpendicular distance R is .