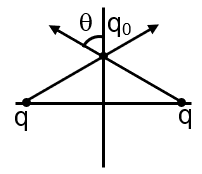
This problem involves electrostatics and small oscillations. We have two fixed charges $q$ at positions $x=-a$ and $x=a$ on the x-axis. A third particle of mass $m$ and charge $q_0=\frac{q}{2}$ is placed at the origin and then given a small displacement $y$ along the y-axis (where $y\ll a$). We need to find the net force on this particle and see what it is proportional to.

Step 1: Visualize the Setup

Let's sketch this out. The two fixed charges are at (-a, 0) and (a, 0). The test charge q₀ is initially at (0, 0). After a small displacement, its new position is (0, y).

Step 2: Calculate the Net Force on q₀ at (0, y)

The net force on q₀ is the vector sum of the forces from the two fixed charges. Since the setup is symmetric, we can calculate the force from one charge and double its y-component (the x-components will cancel out).

Let's find the force ${\mathbf{F}}_1$ on q₀ due to the charge at (a, 0). The distance between this charge and q₀ is:

$r=\sqrt{a^2+y^2}$

The magnitude of the force is given by Coulomb's law:

$F_1=\frac{1}{4\pi {ϵ}_0}\frac{q\cdot q_0}{r^2}=\frac{1}{4\pi {ϵ}_0}\frac{q\cdot \left(\frac{q}{2}\right)}{a^2+y^2}$

This force acts along the line joining the two charges. We need to find its y-component. Let $\theta$ be the angle this force vector makes with the x-axis. From the geometry of the right triangle:

$\sin \theta =\frac{y}{r}=\frac{y}{\sqrt{a^2+y^2}}$

The y-component of ${\mathbf{F}}_1$ is $F_{1y}=-F_1\sin \theta$ (negative because for the charge at (a,0), the force on a positive q₀ at (0,y) pulls it down and to the left).

$F_{1y}=-\left(\frac{1}{4\pi {ϵ}_0}\frac{q\cdot \left(\frac{q}{2}\right)}{a^2+y^2}\right)\cdot \left(\frac{y}{\sqrt{a^2+y^2}}\right)=-\frac{1}{4\pi {ϵ}_0}\frac{q\cdot \left(\frac{q}{2}\right)\cdot y}{{(a^2+y^2)}^{3/2}}$

By symmetry, the force from the charge at (-a, 0) will have the exact same y-component, $F_{2y}=F_{1y}$. The x-components from both forces are equal in magnitude but opposite in direction, so they cancel each other out. Therefore, the net force on q₀ is solely in the y-direction and is given by:

$F_{net,y}=2\times F_{1y}=2\times \left(-\frac{1}{4\pi {ϵ}_0}\frac{q\cdot \left(\frac{q}{2}\right)\cdot y}{{(a^2+y^2)}^{3/2}}\right)=-\frac{1}{4\pi {ϵ}_0}\frac{q^2}{y}{(a^2+y^2)}^{-3/2}$

Step 3: Apply the Small Displacement Approximation (y << a)

The condition $y\ll a$ allows us to simplify the term $a^2+y^2$. Since y² is very small compared to a², we can approximate:

$a^2+y^2\approx a^2$

Therefore,

${(a^2+y^2)}^{-3/2}\approx {\left(a^2\right)}^{-3/2}=\frac{1}{a^3}$

Substituting this back into our net force equation:

$F_{net,y}\approx -\frac{1}{4\pi {ϵ}_0}\frac{q^2}{y}\cdot \frac{1}{a^3}=-\left(\frac{1}{4\pi {ϵ}_0},\frac{q^2}{a^3}\right)y$

Step 4: Final Interpretation

All the terms $\frac{1}{4\pi {ϵ}_0}$, $q^2$, and $a^3$ are constants for this specific setup. Therefore, the net force is:

$F_{net}\propto -y$

The net force acting on the particle is proportional to -y. This is a restoring force (negative sign indicates direction opposite to displacement), characteristic of simple harmonic motion.

Related Topics & Formulae

Coulomb's Law: The force between two point charges $q_1$ and $q_2$ separated by distance $r$ is $\mathbf{F}=\frac{1}{4\pi {ϵ}_0}\frac{q_1{q}_2}{r^2}\hat{\mathbf{r}}$, where $\hat{\mathbf{r}}$ is the unit vector along the line joining the charges.

Superposition Principle: The net force on a charge is the vector sum of the forces exerted on it by all other charges.

Small Angle/Oscillation Approximation: For a small displacement $y\ll a$, terms like $a^2+y^2$ can be approximated to $a^2$ to simplify expressions and reveal linear relationships (like $F\propto y$).

Restoring Force & SHM: A force of the form $F=-ky$ is a restoring force that often leads to simple harmonic motion, where the acceleration $a=-\frac{k}{m}y$.