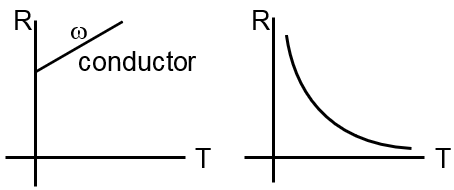
The temperature dependence of resistance differs fundamentally between conductors like copper (Cu) and semiconductors like undoped silicon (Si).

For a conductor such as copper, resistance increases with temperature. This is because the atoms in the lattice vibrate more intensely as temperature rises, which increases the number of collisions experienced by the free electrons that carry the current. This increased scattering reduces the mean free path of the electrons, thereby increasing the resistance. The relationship is approximately linear over a limited temperature range and is given by:

$R=R_0[1+\alpha (T-T_0\left)\right]$

where $\alpha$ is the positive temperature coefficient of resistance.

For an intrinsic (undoped) semiconductor like silicon, resistance decreases dramatically with an increase in temperature. This is because semiconductors have a small energy gap between their valence band and conduction band. At room temperature, very few electrons have enough thermal energy to cross this band gap and conduct electricity. As temperature increases, the number of charge carriers (electrons and holes) increases exponentially. This exponential increase in the number of charge carriers causes the resistivity (and thus resistance) to decrease exponentially. The number of charge carriers $n$ is given by:

$n\propto e^{\frac{-E_g}{2kT}}$

Since conductivity $\sigma$ is proportional to the number of charge carriers ($\sigma \propto n$) and resistance $R$ is the inverse of conductivity ($R\propto \frac{1}{\sigma }$), the resistance decreases exponentially.

Therefore, the correct description is: Linear increase for Cu, exponential decrease for Si.

Related Topics & Formulae

Resistivity and Temperature (Conductors): The resistivity $\rho$ of a conductor is given by $\rho =\frac{m}{n^{2}e\tau }$, where $m$ is electron mass, $n$ is charge carrier density, $e$ is electron charge, and $\tau$ is relaxation time. For conductors, $n$ is nearly constant but $\tau$ decreases with temperature, leading to an increase in $\rho$.

Band Theory and Intrinsic Semiconductors: In semiconductors, the number of intrinsic charge carriers depends on the energy band gap $E_g$ and absolute temperature $T$. The intrinsic carrier concentration is $n_i\propto T^{\frac{3}{2}}{e}^{\frac{-E_g}{2kT}}$. The exponential term dominates, causing a rapid increase in carriers and a corresponding exponential decrease in resistance.