Let f(x) = max {tanx,cotx}. Then number of roots of the equation in (0,.2π) is
If we draw the graph of tan x and cot x, we see that the range of f(x) is
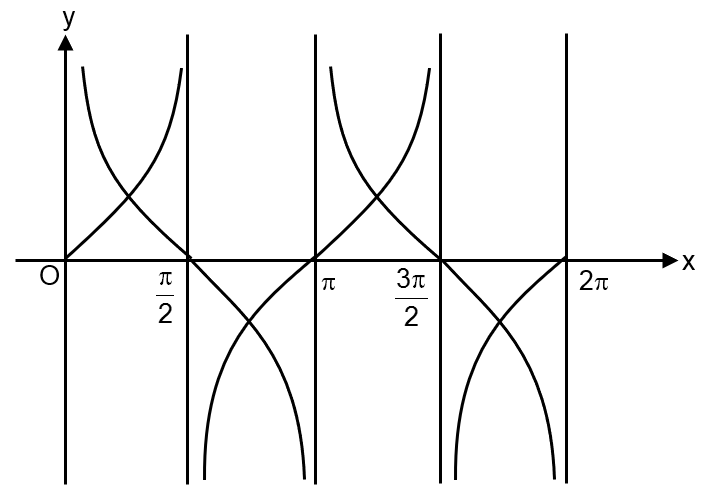
So does not have any root.
Let's analyze the function f(x) = max{tan x, cot x} and solve f(x) = 1/√3 in the interval (0, 2π).
First, recall that cot x = 1/tan x. The function f(x) takes the maximum value between tan x and cot x at each point x.
Step 1: Identify where tan x and cot x are equal. This happens when tan x = cot x. Since cot x = 1/tan x, we have:
⇒ ⇒ or .
In (0, 2π), tan x = 1 at x = π/4 and 5π/4. tan x = -1 at x = 3π/4 and 7π/4.
Step 2: Understand the behavior of f(x). For a given x, if |tan x| ≥ 1, then |tan x| ≥ |cot x|, so f(x) = |tan x| (since max considers magnitude for comparison here, but note: in intervals where both are positive or both negative, the maximum is the larger one; but when they have opposite signs, the positive one is greater). Actually, we need to be careful with signs.
Let's break the interval (0, 2π) into regions based on the sign of tan x and cot x:
But note: f(x) is defined as max{tan x, cot x}, so it takes the algebraically larger value. So in regions where both are positive, f(x) > 1 (except at points where tan x=1). In regions where both are negative, f(x) is negative (since the maximum of two negatives is still negative).
Step 3: Solve f(x) = 1/√3 ≈ 0.577. Since 1/√3 is positive, we only consider intervals where f(x) is positive, i.e., where both tan x and cot x are positive: (0, π/2) and (π, 3π/2).
In (0, π/2): f(x) = max{tan x, cot x}. This function is symmetric about π/4. For x in (0, π/4), tan x < 1 < cot x, so f(x) = cot x. For x in (π/4, π/2), tan x > 1 > cot x, so f(x) = tan x.
Set f(x) = 1/√3:
Wait, check: π/6 is in (0, π/4), but in that subinterval, f(x)=cot x, not tan x. So we should solve cot x = 1/√3 in (0, π/4). cot x = 1/√3 ⇒ tan x = √3, which gives x = π/3. But π/3 ≈ 1.047 > π/4 ≈ 0.785, so it is not in (0, π/4). So indeed no solution in (0, π/2).
Now consider (π, 3π/2): both tan and cot are positive. Let x' = x - π, then x' is in (0, π/2). So behavior is same as (0, π/2). So similarly, no solution in (π, 3π/2).
What about points where tan x = cot x? At x=π/4, f(x)=1. At x=5π/4, f(x)=1. These are not equal to 1/√3.
In negative regions, f(x) is negative, so cannot equal positive 1/√3.
Therefore, there are no solutions to f(x) = 1/√3 in (0, 2π).
Final answer: 0 roots.
This problem involves understanding trigonometric functions, their reciprocals, and the concept of taking the maximum of two functions. Key related topics include properties of tan and cot functions, solving trigonometric equations, and analyzing piecewise functions.