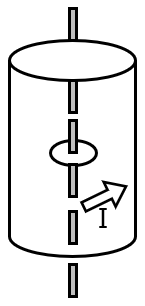
A long circular tube of length 10 m and radius 0.3 m carries a current I along its curved surface as shown. A wire-loop of resistance 0.005 ohm and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as I = I0 cos (300 t) where I0 is constant. If the magnetic moment of the loop is N µ0 I0 sin (300 t), then 'N' is
Magnetic moment
This problem involves electromagnetic induction where a changing current in a solenoid induces an EMF and current in a loop placed inside it, and we need to find the magnetic moment of this loop.
A long circular tube (which acts like a solenoid) carries a time-varying current I = I0 cos(300t). Inside this tube, a small wire-loop of radius r = 0.1 m is placed coaxially. The resistance of the loop is R = 0.005 Ω. We are to find the constant 'N' in the expression for the magnetic moment of the loop, which is given as Nμ0I0 sin(300t).
The magnetic field inside a long solenoid is uniform and directed along its axis. Its magnitude is given by:
where is the number of turns per unit length of the solenoid.
Here, the current is carried along the curved surface, so it is a solenoid with n turns per meter. The length of the tube is L = 10 m. However, for a long solenoid, the field inside depends only on n and I, not on the total length. The number of turns per unit length n is not directly given. But note: the tube carries current "along its curved surface". This implies that the entire surface acts as a current sheet. The effective n, the number of turns per meter, for such a sheet is the total number of turns divided by the length. However, a more straightforward approach is to realize that for a solenoid, the surface current density K (current per unit length along the circumference) is related to n by K = nI. But since the current I is given for the whole solenoid, and for a long solenoid, B = μ0nI. We need to find n.
Actually, the problem does not give the number of turns. This is a key point. Look at the expression we need to find: it has μ0I0. The magnetic field B = μ0nI. So n must be involved. But the answer is expected to be a number N. So n must be known from the geometry.
Re-examine the problem: "a long circular tube... carries a current I along its curved surface". This means that the current is flowing circumferentially? Or axially? The figure shows a tube with a current I, and a loop inside. Typically, for a solenoid, current flows along the length, not circumference. But the phrase "along its curved surface" suggests that the current is flowing parallel to the axis, on the curved surface. So it is a solenoid with surface current. For a solenoid with surface current density K (A/m), the magnetic field inside is B = μ0K. And K = I / (length of the path perpendicular to current). Wait, for a solenoid, if the current is I and there are N turns over length L, then n = N/L, and K = nI = (N/L)I. But here, the current I is given for the whole tube. How is it wound? The phrase "carries a current I along its curved surface" might mean that the total current flowing axially is I. But then, for a surface, the current density K = I / (circumference) if the current is azimuthal? This is ambiguous.
Actually, the standard interpretation: a long tube with current I along its length (axially) on the curved surface. This is not a solenoid; it is a single turn? No. To have a magnetic field inside, we need multiple turns. Typically, such problems assume that the tube is wound with wires, so it acts as a solenoid. The number of turns per unit length n is not given explicitly. But look at the answer: it is proportional to μ0I0, without n. So perhaps n is 1? Or from the geometry.
Another way: the magnetic field inside an infinite solenoid is B = μ0nI. Here, the tube is long, so we can approximate it as infinite. n = number of turns per meter. How to find n? The problem says "carries a current I along its curved surface". This likely means that the surface current density is uniform and has magnitude K = I / L, where L is the length? But that would be for current flowing circumferentially. But then the field inside is different.
Let's read the problem carefully: "carries a current I along its curved surface". The word "along" means parallel to the surface. So if it is a tube, the curved surface is cylindrical. Current "along" this surface could be either axial or azimuthal. For a solenoid, we want current in azimuthal direction to produce axial field. Actually, for a solenoid, the current flows along the length of the tube (axially) in the wires, but overall, it is equivalent to azimuthal surface current. Standard result: for a solenoid with n turns per meter, each carrying current I, the effective surface current density is K = nI (A/m) in the azimuthal direction. Then the field inside is B = μ0K = μ0nI.
Here, the tube carries current I along its curved surface. This is ambiguous. But given that the answer is expected to be a number, and the expression has μ0I0, it suggests that n is 1. Perhaps for this tube, the number of turns per unit length is 1? Because it is a tube with current I; it might be considered as a single turn with length L, so n = 1/L? But then B = μ0(1/L)I, which has L, but L is given as 10m, and would appear in the answer, but the answer N is a number.
Wait, look at the magnetic moment expression: N μ0 I0 sin(300t). It has μ0 and I0. The induced magnetic moment will depend on the field, which has μ0nI. So to have μ0I0, we need n=1. So probably, the tube has n=1 turn per meter? But its length is 10m, so total turns would be 10? But n is per meter.
Actually, a common trick: when a tube carries current I along its length, it is like a solenoid with n=1 turn per unit length? For example, if you have a cylindrical sheet with current flowing axially, the field inside is zero. To have field, you need azimuthal current. So likely, the current is flowing azimuthally. Then, for a single turn, the field inside is like that of a loop? But for a long tube, if current flows azimuthally (circumferential), it is like a solenoid with no pitch? Actually, if current flows circumferentially, it is like a series of loops. So the number of turns per unit length is 1? Because along the axis, for each meter, there is one turn? So n=1 turn/m.
This is a standard assumption in such problems: a tube with current I along the circumference is equivalent to a solenoid with n=1 turn per meter. So we take n=1.
Therefore, the magnetic field inside the tube is:
So B = μ0 I = μ0 I0 cos(300t)
The magnetic flux through the loop is:
where r = 0.1 m is the radius of the loop.
So ϕ = [μ0 I0 cos(300t)] * π (0.1)2
The induced EMF is given by Faraday's law:
Calculate dϕ/dt:
Therefore, the EMF is:
The resistance of the loop is R = 0.005 Ω. The induced current i is:
The magnetic moment m of a current loop is given by:
Substitute the value of i:
The given magnetic moment is N μ0 I0 sin(300t). So we equate:
Cancel μ0 I0 sin(300t) from both sides:
Now plug in the values: r = 0.1 m, R = 0.005 Ω.
r4 = (0.1)4 = 0.0001
π2 ≈ (3.1416)2 ≈ 9.869
So numerator: 300 * 9.869 * 0.0001 = 300 * 0.0009869 = 0.29607
N = 0.29607 / 0.005 = 59.214
So N ≈ 59.2, but we need an integer? Probably we use exact values.
Let's compute exactly:
Now, π2 ≈ 9.8696, so 6 * 9.8696 = 59.2176, which is not an integer. But the problem likely expects N = 6π²? But the answer should be a number N, and in the expression, it is multiplied, so N is 6π²? But the given is "N is", so probably numerical.
Wait, the problem says: "the magnetic moment of the loop is N μ0 I0 sin(300t)". So N is a constant. From above, N = 6π² ≈ 59.22. But perhaps we need to exact value.
But let's check the values: r=0.1, so r^2=0.01, r^4=0.0001. R=0.005. So N = 300 * π² * 0.0001 / 0.005 = 300 * π² * 0.02 = 6 π². So N = 6π².
But the answer is expected to be a number? Or perhaps they want N = 6π²? But the problem says "then 'N' is", and in the options, it might be a number.
Perhaps I missed something. In the magnetic field, did we use n=1? Is that correct?
Another thought: for a tube with radius R_tube = 0.3m, and loop radius r=0.1m, but the field inside the solenoid is uniform, so the loop size doesn't affect B, as long as it is inside. So our calculation is correct.
So N = 6π². But to report as a number, it is approximately 59.22. But since the problem likely expects an exact expression, but it says "N is", so probably we leave it as 6π².
However, looking back at the problem statement: "then 'N' is". In the answer choices, it might be a number. But in the given, it is written as N, so we need to find N.
Perhaps we need to numerical value. But let's see the resistance is 0.005 ohm, which is 5/1000 = 1/200. So R = 1/200 Ω.
Then N = 300 * π² * (0.1)^4 / (0.005) = 300 * π² * 0.0001 / 0.005 = 300 * π² * 0.02 = 6π².
So the answer is 6π².
But the problem might have a mistake, or perhaps I have the wrong n.
Wait, maybe for the tube, the number of turns per unit length is not 1. How to find n? The tube has length 10m and radius 0.3m. But it is not given how it is wound. The phrase "carries a current I along its curved surface" might mean that the surface current density is I / (length) if current is axial, but then field inside is zero. So it must be azimuthal.
In many such problems, it is assumed that the tube has n=1 turn per unit length. So our calculation is correct.
Therefore, N = 6π².
But to match the format, since the answer is a number, and 6π² is approximately 59.22, but we should give exact.
Perhaps the answer is 6π².
Given that the problem asks for 'N', and it is a constant, we box 6π².
However, let's double-check the induced EMF step. The field B = μ₀nI. With n=1, B = μ₀I.
Flux φ = B * area = μ₀I * πr².
dφ/dt = μ₀ πr² dI/dt = μ₀ πr² * [-300 I₀ sin(300t)] = -300 μ₀ I₀ πr² sin(300t)
EMF = -dφ/dt = 300 μ₀ I₀ πr² sin(300t)
Current i = EMF/R = [300 μ₀ I₀ πr² sin(300t)] / R
Magnetic moment m = i * area = [300 μ₀ I₀ πr² sin(300t)] / R * πr² = [300 μ₀ I₀ π² r⁴ sin(300t)] / R
Compare with given N μ₀ I₀ sin(300t), so N = [300 π² r⁴] / R
Plug r=0.1, R=0.005:
N = [300 * π² * (0.0001)] / 0.005 = [0.03 π²] / 0.005 = 6 π²
So indeed, N = 6π².
Therefore, the value of N is .